La matematica applicata al pattinaggio

 

Indice:

Introduzione

Prima parte: Simmetria

Seconda parte: Antimetria

Terza parte: Principio di dualità

 

INTRODUZIONE

Un mio collega, quando seppe che stavo scrivendo un libro di matematica applicata al pattinaggio, mi mandò per email un problema che aveva tentato di risolvere qualche anno fa, immaginando che fosse di un genere analogo a quello degli argomenti trattati nel mio libro, anche se riguardava un’altra disciplina sportiva, il nuoto: rappresentando il busto e le braccia di un nuotatore con un opportuno corpo rigido si era proposto di ricavare la velocità che il nuotatore può raggiungere a partire dal movimento delle braccia, le cosiddette “bracciate”. In pratica pensava che io avessi risolto un problema simile nel pattinaggio, ovvero quello di calcolare la velocità di un pattinatore a partire dal movimento delle gambe, il passo spinta. Ma il mio libro non contiene calcoli o formule matematiche comprensibili solo agli addetti ai lavori! Si propone un compito molto più arduo e ambizioso: quello di convincere i “non credenti”, coloro cioè che sono convinti di non capire la matematica, che ragionare come insegna la matematica può servire a risolvere problemi che apparentemente con questa disciplina non hanno nulla a che fare! D’altra parte, pensate a un ballerino giamaicano che gira sui pattini seduto sulle punte: se gli spiego l’equazione del suo moto rotatorio e il motivo fisico che gli permette di rimanere in equilibrio sulle ginocchia mentre ruota, non gliene importa più di tanto…; se invece gli suggerisco dei nuovi trick, cioè dei nuovi giochi di destrezza che può realizzare grazie alla sua abilità, attiro sicuramente la sua attenzione e conquisto la sua stima. Poi però gli confesso che questi trick non sono merito della mia fantasia, ma del metodo applicato che è stata la matematica a insegnarmi: così, magari, prende più in considerazione la nostra disciplina pentendosi di averla trascurata a suo tempo! Tutto ciò per mettere in evidenza che la matematica non insegna solo a fare i calcoli, ma fornisce anche un metodo, insegna a ragionare in un certo modo per risolvere un problema, non necessariamente matematico. Io ho ragionato matematicamente per risolvere un problema non matematico. La disciplina dello Styleslalom consiste nel realizzare delle evoluzioni con i pattini in mezzo a dei piccoli ostacoli, conetti o bicchieri rovesciati, disposti in linea retta a ugual distanza gli uni dagli altri, solitamente su tre file a 50, 80 120 cm. Le evoluzioni costituiscono i passi e, per ogni passo, si possono mettere in evidenza delle proprietà, quali la simmetria, la periodicità, l’antimetria, definendo il passo inverso, l’opposto, il duale,… Poi a ogni passo si può associare un grafico che riassuma matematicamente queste sue proprietà, senza dover rappresentare necessariamente le traiettorie descritte dai pattini nell’eseguirlo. Un passo si definisce elementare quando non è scomponibile in passi più semplici. Il video seguente ne riporta alcuni esempi.

 

Notiamo che un passo elementare ripete lo stesso andamento ogni due coni. Perciò ad esso si può associare un grafico periodico di periodo T = 2, riportando sull’asse orizzontale lo spazio percorso con i pattini e scegliendo come unità di misura il numero di coni della fila che vengono attraversati, a mano a mano che si procede dal primo all’ultimo. Ne vedremo alcuni esempi più avanti. Introduciamo ora i tre concetti matematici che possiamo utilizzare per costruire con pochi passi elementari numerosissime coreografie, ovvero passi più complessi.

 

1)SIMMETRIA

Alcuni passi elementari ammettono due versioni di realizzazione, definite uno il passo opposto dell’altro. Ad esempio, per attraversare i coni rimanendo su una gamba sola si hanno due possibilità, usare la gamba destra o sinistra. Esempi di passi di questo tipo e dei corrispondenti opposti sono mostrati nel video seguente:

Altri passi invece ammettono un’unica versione di realizzazione, ad esempio la pattinata classica in cui alternativamente si deve piegare e distendere prima una gamba e poi l’altra, oppure il passo definito “camminata”, che potete vedere nel prossimo video:

 

Chiamiamo non simmetrici i passi del primo tipo e simmetrici quelli del secondo. A un passo simmetrico si può associare un grafico simmetrico rispetto all’asse orizzontale lungo il quale il passo si evolve. Ad esempio, nelle figure 1 e 2 sono riportati i grafici rappresentativi di due passi elementari.

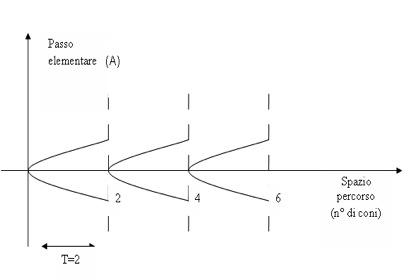
fig.1

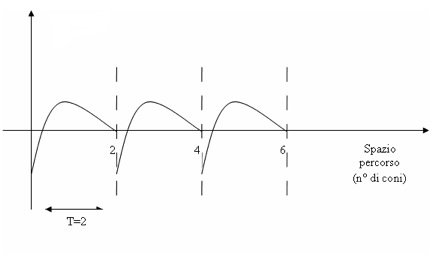
fig.2

Il primo caso (A) riguarda un passo simmetrico in quanto il grafico rimane invariato se si effettua una riflessione rispetto all’asse orizzontale, mentre nel secondo caso (B) abbiamo un passo non simmetrico che quindi ammette opposto, mostrato nella figura 3.

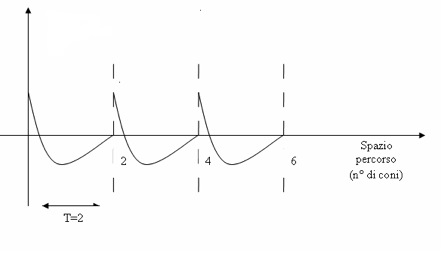
fig.3

Così un passo simmetrico è descritto con un grafico simmetrico rispetto all’asse orizzontale, mentre un passo che ammette opposto viene rappresentato con un grafico non simmetrico e il suo opposto si ottiene mediante una riflessione del grafico originario rispetto all’asse orizzontale.

La cosa interessante è che da un passo elementare non simmetrico si possono creare nuovi passi, non più elementari ma simmetrici, aggiungendogli il suo opposto.

Ad esempio, tornando al passo non simmetrico (B) della figura 2, immaginiamo di realizzarlo solamente nell’intervallo corrispondente al primo periodo di due coni, per poi, cambiando posizione intorno al terzo cono, passare a descrivere il passo opposto di (B), indicato con , nel successivo intervallo di spazio T = 2.

In questo modo si ottiene un passo non più elementare, composto dal passo originario e dal suo opposto, complessivamente simmetrico, di periodo pari a TS = 6. Il risultato è mostrato nella figura 4.

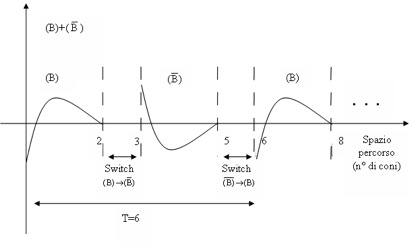
Switch: cambio di posizione

fig.4

Il video seguente riporta esempi di composizioni simmetriche realizzate aggiungendo ad alcuni passi elementari non simmetrici i corrispondenti opposti.

 

Le composizioni simmetriche che si ottengono aggiungendo a uno stesso passo elementare il suo opposto sono più di una. Basta infatti usare switch differenti, cioè realizzare in modo diverso i passaggi tra i due passi.

Ciò è mostrato nei primi due esempi del video 4 che si riferiscono al passo di Ala. Lo switch che permette il passaggio dal passo di Ala al suo opposto nel primo esempio è diverso da quello utilizzato nel secondo caso: in questo modo le composizioni simmetriche che si vengono a formare risultano diverse anche se i passi componenti sono gli stessi.

 

2)ANTIMETRIA

Un altro concetto matematico che possiamo applicare alla teoria dello Styleslalom per costruire nuove coreografie, cioè miscellanee di passi, è quello di funzione inversa. Da un passo elementare A otteniamo il suo inverso A^-1 invertendo i movimenti dei pattini compiuti nell'eseguire A. In pratica se registriamo l'esecuzione di un passo con la videocamera, facendo scorrere indietro il nastro vediamo il suo inverso. L’inverso di un passo può coincidere con il suo opposto, o addirittura con il passo originario. In quest’ultimo caso, invertendo il movimento dei pattini si ottiene ancora lo stesso passo: si parla allora di passo antimetrico.

Nel campo dell’Analisi Matematica una funzione si inverte scambiando le variabili x e y; invece la costruzione di un passo inverso a partire da quello originario si effettua ripercorrendo il grafico in senso contrario cioè dal punto di arrivo a quello di partenza. Il risultato è mostrato con un esempio nelle figure 5 e 6 riportate qui di seguito, dove con (a) si è indicato un passo generico e con (b) il suo inverso, (a)^-1.

 

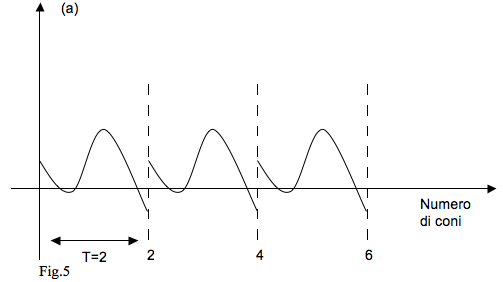
fig.5

 

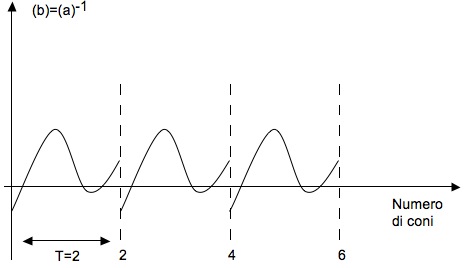
fig.6

In pratica, tutti i valori assunti dal grafico associato a un passo durante la sua evoluzione dall’inizio alla fine di un dato periodo vengono assunti anche dal passo inverso ma al contrario, cioè in ordine invertito. Più semplicemente, l’andamento del passo inverso in un dato periodo si può tracciare facendo una riflessione rispetto all’asse del periodo (vedi fig.7)

 

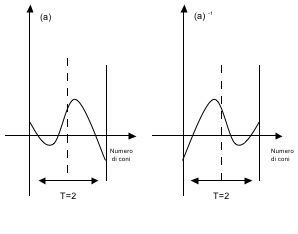
fig.7

Se, effettuando tale riflessione, il grafico rimane inalterato, allora il passo inverso coincide con quello originario. In tal caso il passo risulta, secondo la definizione precedente, antimetrico. Un esempio di passo antimetrico è mostrato nella figura 8.

 

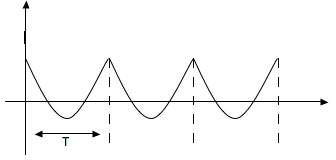
fig.8

Si noti che in Analisi Matematica il termine “antimetrico” non esiste. D’altra parte, mentre esistono passi coincidenti con il proprio inverso, non esistono funzioni coincidenti con la propria inversa (a parte qualche rara eccezione). Infatti il grafico di una funzione nel senso classico del termine (cioè a un sol valore e non polidroma, cioè a più valori) non può rimanere inalterato a seguito di una riflessione rispetto alla bisettrice y = x. In altri termini, l’equazione di una funzione non è più la stessa se scambiamo x con y. L’unica eccezione degna di nota è l’iperbole y = 1/x .

Da un passo elementare non antimetrico si possono creare nuovi passi non più elementari ma antimetrici aggiungendogli l’inverso. Ad esempio, tornando al passo non simmetrico (a) della figura 5, immaginiamo di realizzarlo solamente nell’intervallo corrispondente al primo periodo di due coni, per poi, con un opportuno switch intorno al terzo e quarto cono, passare a descrivere il passo inverso di (a), cioè (a)^-1, nel successivo intervallo di spazio T = 2. In questo modo si ottiene un passo non più elementare, composto dal passo originario e dal suo inverso, complessivamente antimetrico, di periodo pari a T_S = 8. Il risultato è mostrato nella figura 9.

 

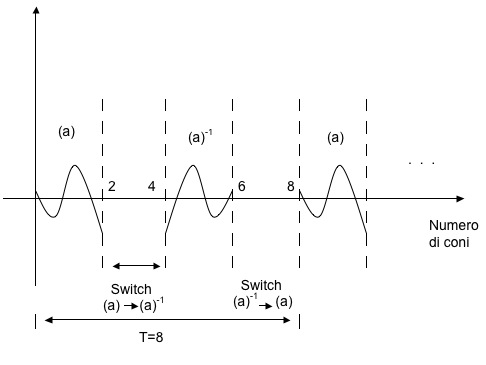
fig.9

Il video seguente mostra un esempio di passo composto antimetrico ottenuto aggiungendo alla camminata avanti il suo corrispondente inverso, ovvero la camminata indietro.

 

 

Esempio:

Verifichiamo che l’inverso dell’opposto di un passo elementare coincide con l’opposto del suo inverso. In formule ciò equivale a scrivere la seguente relazione:

dove si è indicato con A un generico passo elementare.

Consideriamo come esempio di grafico associato al passo elementare A, ancora quello riportato nella figura 5. Dall’andamento di A si deduce quello di tramite una riflessione rispetto all’asse orizzontale e a sua volta dal grafico di  si ottiene poi quello dell’inverso di , ovvero ()^-1, mediante un’ulteriore riflessione rispetto all’asse del periodo T, come mostra la figura 10, dove per semplicità si è limitata la costruzione dei grafici al periodo fondamentale T.

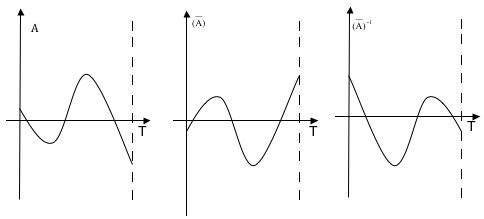
fig.10

Allo stesso modo, sempre rimanendo nel periodo fondamentale T, dal grafico di A si ricava quello di (A)^-1 facendo una riflessione rispetto all’asse del periodo e quindi quello dell’opposto di (A)^-1, cioè , tramite una seconda riflessione rispetto all’asse orizzontale. Il risultato è mostrato nella figura 11.

 

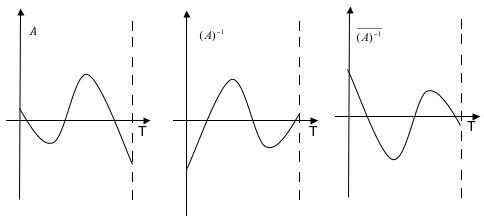
fig.11

Si può notare che l’andamento di , ottenuto nella figura 11, coincide con quello ricavato nella figura 10 per ()^-1. Scegliamo come passo elementare (A) il passaggio nei coni in avanti su una gamba sola, ad esempio la destra, e applichiamo a tale passo le considerazioni precedenti. Invertire (A) significa procedere ancora sulla gamba destra, ma all’indietro, mentre l’opposto dell’inverso, , consiste nell’andare all’indietro ora con la gamba sinistra.

Invece l’opposto del passo di partenza, , si realizza procedendo in avanti tra i coni sulla sola gamba sinistra, e il suo inverso, ()^-1, attraversando i coni all’indietro ancora sulla gamba sinistra. Pertanto si ottiene sempre lo stesso risultato.

 

3)PRINCIPIO DI DUALITÀ

Spesso da una relazione tra certe grandezze se ne può ottenere una seconda altrettanto valida se le grandezze presenti nella prima si sostituiscono con delle altre, dette duali, ricavate secondo opportune corrispondenze. Così, costruendo una tabella che per ogni elemento o grandezza, fornisce il corrispondente duale, da ogni problema si può ricavare e risolvere il suo duale effettuando le corrispondenze dettate dalla tabella. Vediamo qualche esempio.

 

GEOMETRIA

 

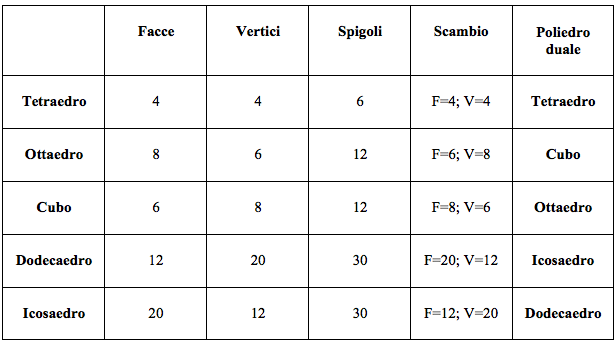
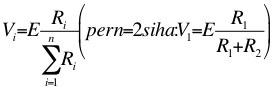
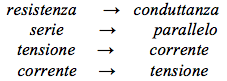
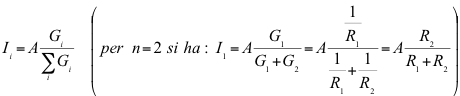
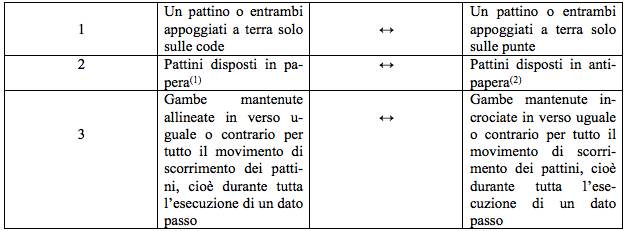
(2)ANTIPAPERA: posizione che si assume disponendo le gambe allineate con i pattini ruotati di 180° l'uno rispetto all'altro ma aventi, a differenza della papera, le code che si guardano in verso opposto.

 

 (I passaggi tra i coni in tali posizioni sono già stati mostrati nel VIDEO 0)

Dato un passo (a) in cui le gambe o i pattini si dispongono secondo almeno una delle tre configurazioni riportate nella colonna di destra o di sinistra, definiamo il suo duale (e lo indichiamo con ) come il passo che otteniamo sostituendo la posizione delle gambe o dei pattini con quella corrispondente presente sulla stessa riga della tabella, ma nella colonna opposta.

Tale duale si dirà del primo, del secondo o del terzo tipo a seconda che la sostituzione corrispondente riguardi la prima, la seconda o la terza riga della colonna. Inoltre il passo duale sarà del primo ordine se si ottiene dal passo originario applicando una sola sostituzione, del secondo ordine o terzo ordine se si effettuano contemporaneamente due o tre sostituzioni, cioè se si applicano due o tre delle corrispondenze riportate in tabella.

Il video seguente riporta per alcuni passi elementari esempi di corrispondenti duali.

 

 In particolare, come primo esempio, viene mostrato il duale del terzo tipo del passaggio tra i coni in papera. Tale passo duale si ottiene applicando la terza corrispondenza della tabella e quindi disponendo le gambe ancora in papera, ma incrociate, anziché allineate. Il secondo esempio mostra il duale, ancora del terzo tipo, dell'attraversamento dei coni con le gambe allineate in tacco punta.

 

Esempio

Consideriamo il passaggio attraverso i coni con i pattini disposti in papera appoggiati a terra solo sulle code e proviamo a costruire:

1. il passo duale del primo ordine del primo tipo
2. i passi duali del secondo ordine, sia del secondo che del terzo tipo, che si ottengono a partire dal passo duale del primo tipo ricavato al punto 1).

 

Soluzione

1. Applicando la prima corrispondenza della tabella si ottiene come passo l’attraversamento dei coni con i pattini ancora in papera, ma appoggiati al terreno sulle punte.
2. Applicando la seconda e terza corrispondenza della tabella al passo duale del primo ordine ricavato al punto precedente si ottengono i passaggi tra in coni in antipapera sulle punte mantenendo le gambe allineate oppure in papera, sempre sulle punte, con le gambe incrociate. Tali passi sono mostrati nel video seguente

 

 

Enrico Perano