.

Un problema elementare

Di Fausto Saleri
(tratto - per gentile concessione dell’editore - da
C. Ciliberto – F. Saleri – E. Strickland, I numeri nel cuore, Springer-Verlag Italia, 2008 pp. 77-98)

Erano da poco passate le undici di quella fresca giornata di primavera inoltrata quando il dottor Gastald, ripuliti e riposti i ferri del mestiere, si era reso conto con sorpresa di non avere più alcun paziente da visitare. Si trattava di una piacevole novità, da prendere però con cautela, visto che nei giorni precedenti era stato letteralmente assediato dalle vittime di un’epidemia di raffreddore provocata da un inatteso abbassamento della temperatura. Prima di esultare volle dunque controllare che non vi fosse proprio nessuno in ambulatorio e, con la scusa di riordinare la piccola stanza che assolveva a quel compito, verificò che fosse completamente vuota. Aprì quindi con circospezione la porta d’ingresso e con grande soddisfazione vide che non v’era neppure l’ombra di un malato. Era libero, libero di rilassarsi finalmente un poco. Rientrò quindi rapidamente solo per dire a Cristine, la sua anziana domestica, che si sarebbe assentato per qualche ora e che non sarebbe ritornato a pranzo. Se ci fosse stato qualche caso urgente che lo mandassero a chiamare, lo avrebbero trovato al negozio del suo migliore amico, mastro Fabrius, e poi alla trattoria. Indossò quindi una giacca leggera ed uscì all’aria aperta per immergersi in quel miscuglio di profumi e suoni caratteristici della stagione primaverile.
            Il lieto garrire dei rondoni che inseguivano qualche insetto al di sopra del suo orto lo accolse festoso, accompagnato dalla fragranza nell’aria dell’erba appena tagliata in un campo poco distante. Uscì dalla cinta del suo giardino con studiata lentezza, deciso ad incamminarsi per un sentiero che, costeggiando il paese dalla parte del bosco, costituiva la via più lunga per arrivare alla casa dell’amico. Girovagò così spensieratamente in campagna per una mezz’ora.
            Un mucchio di terra, smossa di recente per rifare il canale di scolo dell’acqua piovana, gli annunciò il ritorno alla civiltà e la fine imminente della sua passeggiata. Di lì a pochi metri sbucò infatti sulla strada principale e, percorsa un’altra manciata di passi, si ritrovò davanti al negozio dell’amico. Il profumo penetrante di un gelsomino cercò di attirarlo nuovamente verso la campagna, ma la porta, dall’anta solo leggermente accostata, lo invitò ad entrare oscillando leggermente a causa del vento.
            Non appena Gastald sospinse l’uscio un campanello tintinnò debolmente nella penombra che gravava in quel locale. Il dottore si diresse senza indugio verso il bancone di noce, segnato dal tempo, dietro al quale avrebbe dovuto esserci il suo amico.
            “Fabrius, dove siete?” domandò il dottore guardandosi attorno e, non ricevendo risposta, fece rotta verso il retrobottega.
            Se il negozio richiamava una polverosa soffitta con quel suo caotico accatastarsi di manufatti disparati, il locale dove ora si trovava sembrava invece una disastrata libreria: scaffali incurvati dal peso di ponderosi volumi riversavano nella stanzetta cascate di fogli di varie dimensioni e tipi, gran parte dei quali vergati nell’incomprensibile scrittura dell’amico. E se in alcuni si potevano riconoscere delle distinte, altri parevano riportare misteriose iscrizioni in lingue ormai dimenticate.
            “Non toccate nulla, ve ne prego” lo apostrofò Fabrius che, seduto davanti a un tavolino, stava scrivendo freneticamente qualcosa. Gastald sollevò le mani a far capire che non intendeva turbare in nessun modo la sua attività.
            “è questione di pochi minuti” commentò l’altro senza alzare il naso dalle carte, “sto facendo quadrare i conti di questo mese, ma c’è qualcosa che non torna. è una faccenda di metodo e di aritmetica: qua ci sono le spese, là le vendite, dopo di che si tratta soltanto di eseguire qualche somma e sottrazione. Immagino che anche voi abbiate un archivio come il mio” proseguì l’uomo, quasi con orgoglio, sbirciando in alcuni foglietti infilzati in uno spillone. Il dottore, che si faceva aiutare per la contabilità dal figlio del farmacista, si augurò che i suoi libri contabili non assomigliassero neppure lontanamente a quel guazzabuglio che lo circondava, ma non volle commentare. D’altra parte ognuno ha il suo ordine e quel che disorienta uno, rassicura un altro, pensò, cercando al contempo una superficie libera sulla quale sedersi.
            “Perché invece di scalpitare come un cavallo impaziente non mi aiutate controllando queste somme?” domandò Fabrius che lo stava osservando.
            “Se proprio devo… io e l’aritmetica non siamo molto affiatati” fu la laconica risposta di Gastald che, avendo rinunciato all’improba impresa di trovare un posto dove sedersi, prese a scorrere mal volentieri l’elenco di cifre. In effetti tra lui e i numeri c’era sempre stata una sostanziale antipatia fin dai tempi della giovinezza, quando il severo maestro elementare lo obbligava a scrivere infinite enumerazioni. Questa latente ostilità si era con il passare degli anni rafforzata ed aveva finito per far sì che il dottore associasse ai numeri solo pensieri negativi. Erano loro che al giovane studente universitario ricordavano la cronica mancanza di denaro o i voti negli esami ed erano ancora i numeri, graziosamente inquadrati nei foglietti del calendario, che al maturo dottore dicevano che il tempo stava inesorabilmente passando e che qualche capello bianco si sarebbe fatto strada nella sua folta capigliatura. Più e più volte, nel tentativo di risollevare quel rapporto, si era detto che non si trattava che di simboli, esattamente come le lettere dell’alfabeto e che, come quelle, opportunamente combinati formavano delle espressioni, ma il termine stesso di espressione stonava nella sua mente, quasi fosse un abuso, una volta che fosse riferito ad una successione di operazioni e numeri.
            “Ecco, tenete, avevate sbagliato un riporto. è facile distrarsi quando si svolgono compiti così noiosi come sommare o sottrarre delle cifre” disse dopo che fu passato qualche minuto restituendo un foglietto a Fabrius. Quello, osservato l’errore, si passò una mano sulla fronte scuotendo la testa.
            “Avete ragione, come ho fatto a non accorgermene! Grazie mille amico mio” rispose alzandosi e stiracchiandosi un poco. “Non vi ho neppure chiesto perché siete qui e a quest’ora poi!” proseguì dopo aver notato con sorpresa l’orologio.
            “Si direbbe che fortunatamente oggi nessuno abbia bisogno dei miei servigi”, rispose il dottore. “Pensavo allora di invitarvi a mangiare qualcosa di buono, condendo il nutrimento con dell’ottimo vino e delle chiacchiere, spero anche migliori. Ma se siete occupato…” concluse allargando le braccia e inarcando le sopracciglia.
            Fabrius gli fece un largo sorriso, si mise la giacca che se ne stava appoggiata sulla spalliera della sedia dove era stato seduto per poi, presolo sottobraccio, dirigersi verso l’uscita del negozio.
            “I conti possono aspettare. Mi dicono invece che la moglie dell’oste ha cucinato un’oca al forno con le mele che non può attendere” rispose chiudendo a chiave la porta del negozio.
            Era da poco passata l’una e, come sempre accade nelle giornate calde e con poco vento, il cielo si era leggermente velato, assumendo una tonalità turchina particolarmente chiara, quasi bianca. A parte i due amici, non c’era nessuno per strada e solo l’instancabile frinire delle cicale, nascoste sui platani della piazza principale, teneva loro compagnia.
“Una pace così è degna del Paradiso terrestre” disse il dottore rompendo il silenzio.
        “Verissimo” rispose Fabrius, “ed ecco infatti un angelo che arriva” riprese indicando a Gastald una elegante figura che avanzava verso di loro da un angolo della piazza. Al dottore il cuore prese a battere più intensamente perché non ci si poteva sbagliare, l’angelo di cui parlava Fabrius era la signorina Louise, la maestra elementare del paese che tanto spazio occupava nei suoi pensieri e nel suo cuore. La giovane donna si era fatta vicina e il dottore poteva percepirne il profumo raffinato e semplice al contempo e già i suoi occhi non vedevano altro se non quei capelli accarezzati dai raggi del sole, catturati qua e là dalle larghe foglie dei platani.
          “Oh, Maurice, è il cielo che vi manda, ho un problema da sottoporvi” disse Louise non appena si fu avvicinata e li ebbe salutati. Avrebbe voluto dirle che lei era una celeste apparizione, ma Maurice Gastald, frenato da una strana forma di pudore, si limitò a dirle che era a sua completa disposizione e mai affermazione fu più appropriata.
            “Stavamo andando a pranzo” intervenne Fabrius con gentilezza. “Volete unirvi a noi?”
         “Vi ringrazio ed accetterei volentieri l’invito, ma ho già mangiato qualcosa proprio per potermi subito dedicare al problema cui accennavo. Sapete, stamattina ho assegnato un compito ai miei scolari per tenerli impegnati, sono tanto turbolenti…”’ sospirò , “ma ne ho sottovalutato la difficoltà e non vorrei trovarmi domani in crisi di fronte a loro. Sono molto preoccupata. Potreste ascoltarmi dopo pranzo, Maurice?” chiese sbattendo leggermente le palpebre e Gastald, perso in quello sguardo, vide chiaramente l’oca al forno della signora Berthame che, dopo aver miracolosamente riacquistato penne e piume, si stava allontanando alta nel cielo, non senza averlo prima salutato con la punta di un’ala.
            “A ben pensarci sarà meglio per me non pranzare oggi, visto il mio profilo che diventa di giorno in giorno più prominente!” rispose il dottore sorridendo. “Se non vi spiace, Fabrius, vi abbandono ai piaceri culinari per fermarmi con Louise e capire come posso aiutarla” soggiunse mettendosi al fianco della ragazza sorridente.
         Restati soli, Louise e Maurice si accomodarono su una semplice panchina di legno, addossata al tronco marezzato di un enorme platano.
             “Siete molto gentile a rinunciare all’oca di Madame Berthame per me” disse Louise con quella dolcezza che sempre la caratterizzava, ma sorprendendo non poco Gastald che non ricordava d’aver parlato del succulento animale. “E non fate quella faccia! Non serve essere indovini per associare il profumo che da stamattina ha messo l’acquolina in bocca a tutto il paese ad uno dei piatti più ricercati della trattoria. E tenendo conto di quanto voi ed il vostro amico siete buongustai, non potevo sbagliarmi immaginando che proprio quello avreste mangiato” concluse abbassando impercettibilmente il capo.
           “Ma non divaghiamo di cibi e deduzioni, vi espongo il mio problema: si tratta di una questione di aritmetica che a voi, che siete uomo di scienza, apparirà forse come un giochino”, disse la maestra estraendo un foglietto da una tasca della sua gonna bianca, decorata da fiorellini del colore dei suoi occhi. Gastald impallidì; sperava si trattasse di un qualche quesito di scienze o letteratura; anche la grammatica, magari latina, sarebbe stata ben accetta, ma la matematica…
         “Dite pure, adoro gli enigmi” rispose dicendo una mezza verità visto che amava veramente i misteri, ma purché non fossero formulati in termini numerici.
          “Se vi chiedessi di calcolare la somma dei numeri da 1 a 3, cosa mi direste?” gli domandò senza esitazioni la maestra.
              “Dunque, 1 più 2 più 3: 6!” rispose il dottore con calma.
              “E da 1 a 4?” e poi, prima che il dottore potesse rispondere, proseguì: “E da 1 a 100 o da 1 a 1000?”. Gastald corrugò la fronte, ci sarebbero volute ore, forse giorni per eseguire quei conti, senza considerare gli eventuali errori, rispose.
           “Ed invece non è così. Ho infatti letto da qualche parte che esiste una formula che permette con pochissime operazioni di trovare il risultato” rispose la maestra. “Il problema è che non solo non me la ricordo e non riesco a ricavarla, ma ho sventatamente assegnato ai miei studenti il compito di trovarla. Capite subito quanto sia preoccupata. Cosa dirò loro domani quando mi chiederanno la soluzione? O semplicemente, come potrò controllare che eventuali soluzioni da loro proposte (non ci conto, ma potrebbe accadere) siano giuste?” proseguì Louise angosciata. “Dovete aiutarmi, Maurice. Io non ho fatto altro che pensare a questo da stamattina, ma senza giungere a nessuna conclusione.”
             “Mia cara, non preoccupatevi, ho davanti a me tutto il pomeriggio e sono certo di poter risolvere il vostro problema. Mi chiuderò nel silenzio del mio studio dove nessuno verrà a disturbarmi” rispose il dottore alzandosi in piedi all’improvviso e facendo così sfuggire un gruppetto di passeri che si era loro avvicinato a caccia di qualche briciola da beccare.
                In un momento, dopo aver salutato una Louise sollevata da tutta quella sicurezza, si ritrovò seduto nel suo studio, davanti allo scrittoio sul cui piano aveva allineato alcuni fogli ed una matita perfettamente temperata. Gli pareva di essere tornato a scuola, di ritrovare quella tensione che sale inesorabilmente di fronte ad una prova scritta, soli con se stessi ed il quesito proposto. E, come a scuola, ricopiò in bella calligrafia su un foglio intonso il suo quesito: quanto vale la somma dei numeri da 1 fino ad un numero dato? E subito sotto, bene al centro, scrisse Soluzione. Dato che da qualcosa bisognava pur partire riportò anche la prima delle somme che avrebbe dovuto calcolare, 1+2=3, per poi aggiungervi accanto 1+2+3=6 ed avrebbe proseguito se la punta del lapis non gli si fosse spezzata. ‘Cose che capitano’ pensò prendendo immediatamente il coltellino che fungeva da temperamatite, ma mentre affilava la punta rifletté che il suo scopo non era quello di calcolare quante più somme fosse possibile, bensì di trovare una formula che gli permettesse di trovare il risultato con pochissime operazioni. Se fosse riuscito in quella sintesi avrebbe scoperto qualcosa di nuovo, si ritrovò a pensare con orgoglio: la formula di Gastald avrebbero potuto chiamarla, ma si ricordò con disappunto che Louise aveva letto da qualche parte di quella ingegnosa trovata; lui si sarebbe dunque limitato a riscoprirla. Il lato pragmatico del suo carattere gli suggerì che sarebbe stato comunque un successo rilevante, se non addirittura obbligatorio, viste le attese di Louise e con sorpresa si trovò a pensare che stava provando piacere nell’accingersi a quell’impresa nella quale avrebbe manipolato solo dei numeri. Forse che la matematica non fosse tanto noiosa come gli era sempre apparsa?
                Senza darsi una risposta, riprese in mano il foglio analizzando le somme che aveva ottenuto nella speranza di trovarvi la regola che cercava: la prima osservazione che fece fu che le due somme, 3 e 6, erano i primi due multipli di 3. La formula di Gastald gli si rivelò radiosa: per sommare i numeri da 1 ad un numero dato basta considerare il numero degli addendi, diminuire questo numero di 1 e moltiplicarlo per 3. In effetti sommando i primi due numeri interi si trova 3, ossia proprio 2-1 per 3. Allo stesso modo la somma dei primi tre numeri è proprio 3-1 per 3, cioè 6.
            L’entusiasmo crebbe a dismisura e si vide in quel momento come un novello Archimede, pronto a balzare fuori della vasca gridando “Eureka!” per le vie del paese. Gli venne da ridere immaginandosi la scena di lui, nudo, di corsa per strada; chissà cosa avrebbero pensato Cristine o le altre ben pensanti del paese!
              Una sana prudenza gli intimò per lo meno una verifica della sua mirabolante scoperta. La matita venne temperata ed una nuova somma si aggiunse alle precedenti: 1+2+3+4=10. Se la formula di Gastald fosse stata vera, 10 avrebbe dovuto essere pari a 4-1 per 3 che però si ostinò a fare rigorosamente 9 e venne perciò scritta sul foglio accompagnata da un plotone di punti esclamativi. Una frase sentita tante volte, ‘l’eccezione conferma la regola’, gli risuonò per un momento in capo e solo allora si chiese che senso avesse veramente quella affermazione in aritmetica.
              Passato il primo momento di sconforto ed osservato che in fondo non era trascorsa che un’ora da quando aveva lasciato la maestra, si rimise a pensare. ‘Era solo il primo tentativo in fondo’ meditò osservando al contempo che la formula trovata non era poi così malvagia. ‘Certo, 9 non è 10, ma non è molto lontano’ si disse, convincendosi che si trattava di aggiustare un poco la sua ricetta. Sommare semplicemente uno non avrebbe però funzionato, perché avrebbe sì fatto tornare l’ultimo risultato, ma non tutti i precedenti. Doveva servire qualcosa di più complicato, rifletté passandosi la matita fra i capelli.
               Dopo dieci minuti di inutili riflessioni e di fogli accartocciati nel cestino, Gastald decise che quella stanza si era fatta troppo calda. ‘Manca l’ossigeno e senza di esso il cervello non funziona’, concluse spalancando la finestra che dava sull’orto. Un refolo d’aria, pervaso dal profumo della menta piperita che spuntava al margine del muretto, penetrò nello studio. Gastald respirò profondamente con le mani appoggiate sul davanzale, mentre delle rondini inscenavano dei volteggi acrobatici di fronte ai suoi occhi. Rinfrancato, decise di ripartire da capo alla ricerca di un’idea totalmente diversa. Prese dunque un nuovo foglio dalla pila ormai assottigliata e, rifatta la punta alla matita che pure si stava decisamente riducendo in lunghezza, decise di scrivere le odiate somme non affiancate, ma una al di sotto dell’altra. In breve, quasi al centro del foglio si disposero i seguenti calcoli:

1+2=3

1+2+3=6

1+2+3+4=10

1+2+3+4+5=15.

  Vedendoli scritti in questo modo si diede una manata in fronte: come aveva fatto a non notare prima che la somma successiva si otteneva dalla precedente semplicemente aggiungendo a quella l’ultimo numero! Era un’osservazione banale, ovvia, al limite della stupidità che tuttavia lo riempì di speranza: era forse questo il segreto della formula che con poche operazioni gli avrebbe permesso di trovare quelle somme infernali? A ben guardare, questo modo di procedere prevedeva di conoscere già il valore della somma appena precedente a quella che si intendeva trovare, informazione che non avrebbe avuto se gli avessero chiesto di calcolare, ad esempio, la somma dei primi cento numeri. Anche questa strada non sembrava dunque condurlo da nessuna parte.
           Il caldo gli sembrava nel frattempo aumentato, fatto strano visto che generalmente con il procedere del pomeriggio l’aria rinfresca. Il pensiero che quella sera avrebbe dovuto innaffiare l’orto o i suoi pomodori non sarebbero mai germinati gli passò per il capo, scacciato al volo visto che l’orologio aveva inesorabilmente spostato le sue lancette sulle cinque e mezza.
           ‘Tempus fugit’ si disse riportando su un altro foglio, girato questa volta per il lungo, solo il risultato delle operazioni fatte, 3, 6, 10 e 15, scritti in grande in modo da risultare ben visibili al centro della pagina. Quel quindici in ultima posizione lo colpì: ancora un multiplo di tre! E se anche la somma successiva lo fosse stata? E quasi non osava scriverla per paura di trovare un risultato di quel genere. Si fece forza ed in basso alla pagina vergò un 1+2+3+4+5+6=21. Di nuovo l’insulsa frasetta dell’eccezione che conferma la regola gli echeggiò dentro, ben più rumorosa di quel maggiolino che sentiva ronzare fuori dalla finestra. Certo, a ben guardare 15 non era quel che avrebbe dovuto essere, secondo la formula da lui congetturata, ed anche 21 non era corretto, ma erano pur sempre tutti multipli di 3. Ah, se non ci fosse stata quella somma intermedia pari a 10! Se avesse potuto cancellarla avrebbe forse fatto un passo decisivo verso la soluzione di quell’enigma. E del resto, anche la somma successiva pari 21+8 era ancora divisibile per 3, ma non poté indagare ulteriormente la portata delle sue ultime scoperte perché la porta del suo studio si aprì.
           “Caro Maurice, cosa vi siete perso!” esclamò Fabrius entrando “Anzi, è meglio per voi non saperlo proprio! Voglio solo dirvi che per digerire l’animale e il nettare di Bacco che lo ha accompagnato ho dovuto farmi un monumentale pisolino, terminato solo una ventina di minuti fa”, concluse mettendosi a sedere beato. Il dottore lo salutò con un cenno, mantenendo il capo chino sul tavolo.
             “Anche voi impegnato a sistemare la contabilità?” gli chiese avvicinandosi per prendere in mano un foglio sul quale alcuni numeri erano stati prima collegati con delle frecce e poi parzialmente cancellati da un ghirigoro formato da una linea intrecciata.
            “Non esattamente, anzi per niente. Si tratta solo di un gioco che ho iniziato giusto per ingannare il tempo, Ma ditemi, l’oca era squisita come si poteva intuire dal profumino?” rispose con non poco imbarazzo cercando di nascondere i suoi calcoli e di indirizzare altrove la conversazione. Fabrius, che era curioso come un gatto, non si lasciò distrarre:
           “Interessante. E di che gioco si tratta? Scacchi, dama carte? Forse anagrammi? No, fatemi indovinare: una frase crittografata! È questo vero? Ecco il perché di tutti questi numeri. Dunque, 3, 6, 10, 15. 21; si tratta certamente della chiave del testo che intendete decifrare. Amico mio, siete fortunato, non solo ho una propensione naturale a risolvere questo genere di indovinelli, ma dovete sapere che mio zio lavorava al servizio cifra dell’esercito e mi ha insegnato tutti i loro trucchi quand’ero ragazzo. Immagino che abbiate già provato ad associare ad ogni numero una lettera dell’alfabeto.”
             Gastald avrebbe voluto fermare l’amico almeno per dirgli che era sulla strada sbagliata, ma quello era ormai scatenato e stava già scrivendo qualcosa su un pezzo di carta.
             “Bisogna innanzitutto riportare l’alfabeto: A, B, C, D, E, F, G, H, I, J, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z. A questo punto scriviamo sotto ogni lettera un numero partendo dalla A e vediamo se la vostra sequenza di numeri diventa una parola di senso compiuto. Si trova CFJPV che, però, non mi dice nulla. E probabilmente anche voi sarete arrivato a questa conclusione e vi sarete disperato. Ed è proprio in frangenti come questo che ci vuole la mano dell’esperto” proseguì sorridendo Fabrius. “Dovete sapere che già al tempo dei romani si usava intercettare la corrispondenza altrui e Giulio Cesare, che era uno che aveva parecchie cosucce da nascondere, si cautelava opportunamente” riprese, mentre il dottore, che vedeva il tempo scorrere in modo pericoloso, avrebbe fatto a meno di questa divagazione storica.
           “E come faceva il grande dittatore a cifrare i suoi scritti? Associava ad ogni lettera dell’alfabeto latino un numero, partendo da una lettera scelta a caso e poi proseguendo ordinatamente. Giunto all’ultima lettera ripartiva dalla prima. In questo modo i testi diventavano una successione di numeri che solo chi era a conoscenza della giusta corrispondenza poteva decifrare” concluse con entusiasmo rivolto ad un rassegnato Gastald. “Ad esempio, supponiamo di associare* il numero 1 non alla lettera A ma alla Z, di associare 2 alla A e poi di procedere come prima. Troviamo BEIOT, parola decisamente più interessante, non trovate? Tanto per cominciare è un cognome, ma se non vi dice nulla non è questa la strada giusta.”
               Gastald scosse il capo, era venuto il momento di interrompere quella assurda ricerca. “Zitto, state zitto, come il sacrestano muto di Don Maritain: sento infatti che l’illuminazione è arrivata” lo interruppe Fabrius con aria mistica prima che il dottore potesse intervenire. “Avete di fronte a voi un genio dell’enigmistica: BEIOT è l’anagramma di BOITE! Si tratta di un testo crittografato e anagrammato, un vero capolavoro insomma, ma non per degli esperti come il sottoscritto” esclamò scrivendo su un foglio a caratteri cubitali, seppur sgraziati, la parola boite. “Mostratemi il resto del testo e procediamo” riprese, non poco meravigliato dell’assenza di entusiasmo manifestata dal dottore il quale, solo allora, riuscì finalmente a parlare:
             “Fabrius, vi ringrazio per l’impegno, ma non è un anagramma, un crittogramma o un rebus. Sono alcuni numeri legati al problema che mi ha sottoposto oggi Louise, quando l’abbiamo incontrata. Si tratta, vedete, di un problema di aritmetica” e disse quest’ultima frase con un tono quasi impercettibile.
              “Un problema di aritmetica! Per voi! Che odiate i numeri!” esclamò Fabrius soffocando le risate e lasciandosi cadere su una poltrona, mentre il suo volto assumeva delle tonalità fra il rosso ed il violaceo. “È troppo divertente, mi farete morire” continuò di fronte a un Gastald sempre più contrariato.
             “Se avete finito di ridacchiare alle mie spalle, avrei del lavoro da fare” gli disse quello rimettendo in ordine i fogli sulla scrivania. Fabrius riacquistò immediatamente un contegno più consono al dramma che l’amico stava vivendo:
              “Suvvia, stavo solo scherzando” disse. “Se volete, posso provare ad aiutarvi, anche se la mia non è una mente portata per la più arida fra tutte le materie.”
             “Amico caro, il problema sembra semplice, e forse lo è, ma mi sfugge la soluzione: si tratta di trovare la somma di tutti i numeri da 1 fino ad un numero fissato che potrebbe però essere assai grande. Bisogna quindi trovare una formula sintetica che permetta di ottenere un risultato rapidamente e con pochi calcoli” spiegò il dottore tutto d’un fiato perché gli sembrava di sprecare tempo.
            Fabrius ci pensò un attimo, torse un poco il collo, quasi volesse liberarsi da un fastidioso dolore, arricciò le labbra per poi, preso un foglio, scrivergli sopra un numero, passando il tutto al dottore.
               “Allora? Che vuol dire questo otto? Sarebbe questa la vostra risposta? Disse Gastald per lo meno perplesso. Fabrius aggrottò le ciglia e senza dire una parola fece eseguire al foglio una rotazione di novanta gradi fra le mani di un sempre più esterrefatto Gastald.
             “La risposta che cercate è infinito, questo è il valore della vostra somma. Per vostra cultura, sappiate che l’otto coricato è il simbolo che si usa in matematica per indicare l’infinito.”
             Gastald non capiva se lo stesse prendendo in giro od introducendo a dei misteri rispetto ai quali quelli Eleusinisarebbero stati robetta per bambini. Di fronte ad un tale smarrimento, Fabrius si sentì in dovere di precisare maggiormente la sua risposta:
             “Supponiamo ad esempio di voler eseguire la somma dei numeri da 1 a 2: sommeremo certamente 1 con 2, ma poi dovremo aggiungervi anche 1.5 che sta fra 1 e 2, e che dire di 1.1, 1.2 e di tutti gli altri numeri decimali compresi fra 1 e 2? E visto che di questi numeri ne avete infiniti la loro somma non potrà che darvi un valore arbitrariamente grande, o, in altri termini, infinito” e, detto questo, si rimise comodamente a sedere, mentre Gastald capiva finalmente l’incomprensione nella quale era caduto l’amico.
           “Fabrius, mi farete venire il mal di testa con le vostre idee, ammesso che già non l’abbia. A me interessa solo la somma dei numeri interi, non di quelli decimali! E poi quel che dite non mi sembra comunque tanto giusto. Mi fate tornare alla memoria i paradossi di Zenone nei quali sommando infiniti passi si percorreva comunque una distanza finita”, rispose il dottore un poco spazientito e per nulla convinto. Fabrius sbuffò sonoramente.
             “Dovevate essere più chiaro allora” riprese grattandosi il capo ì, “e comunque i vostri sofismi non vi porteranno alla soluzione”, concluse infastidito perché si era accorto che qualcosa nel suo ragionamento avrebbe potuto non funzionare. Gastald non ebbe il tempo di replicare perché la porta dello studio si aprì nuovamente per far entrare Cristine, la sua domestica.
            “Dottore, un signore tedesco di passaggio ha bisogno di voi per curarsi un fastidioso mal di denti che lo tormenta. Avrebbe urgenza, se ho capito quel suo orribile francese, perché la carrozza lo aspetta per riprendere il viaggio” gli comunicò gelida, evidentemente seccata da quel contrattempo, per di più ad opera di uno straniero, che l’aveva distratta dalla preparazione della cena.
            “Grazie Cristine. Sarò da lui tra poco. Lo faccia accomodare in ambulatorio”, rispose Gastald che aveva ben altri pensieri per la testa. La vecchia domestica se ne uscì sbattendo la porta meditando, come sempre, su quanto fosse migliore il venerato predecessore di Gastald, il dottor Feraud, che lei aveva umilmente servito per cinquant’anni. ‘Lui non avrebbe medicato un nemico della Francia, anche se anziano’ pensò tristemente, mentre cercava di spiegare allo straniero dai capelli bianchi dove fosse l’ambulatorio.
               Rinchiusasi la porta, il dottore si rivolse nuovamente a Fabrius.
             “Era andata fin troppo bene, dovevo aspettarmi che arrivasse qualcuno ed il tempo a mia disposizione è agli sgoccioli” commentò amaramente osservando come la lancetta corta dell’orologio fosse ormai pericolosamente vicina alle sei. “Prima che arrivaste mi ero fatto una mezza teoria secondo la quale tutti questi numeri sono degli opportuni multipli di 3” aggiunse rivolto a Fabrius e scrivendogli la solita serie di numeri, 3, 6, 10, 15, 21, 29. L’amico osservò i numeri meravigliato.
           “Amico mio, d’accordo che l’aritmetica non faccia per voi e che siete distratto dagli amorosi sensi, ma 10 non è divisibile per 3 e se non mi sbaglio neppure 29!” commentò. “Che volto funereo. Per consolarvi vi dirò che se anche 29 fosse stato divisibile per 3 vi sarebbe servito a poco perché 29 non ha niente a che vedere con gli altri numeri” riprese mettendosi a fare dei conti. “Esattamente. Guardate, è come pensavo: 1+2+3+4+5+6+7=28, non 29. Del resto è normale far di questi errori, quando si svolgono conti tanto noiosi” sibilò ricordando a Gastald le sue stesse parole della mattina. Il dottore era completamente sbiancato e non aveva la forza di reagire perché il duplice errore lo aveva tramortito: non solo la sua teoria si era definitivamente rivelata erronea, ma nel suo amor proprio si era anche aperta una falla di dimensioni notevoli.
              I due uomini stettero così, per una ventina di minuti almeno, perfettamente silenziosi, ciascuno immerso nel proprio stato d’animo: Fabrius prese a svolgere un grandissimo numero di somme nella speranza di capire a forza bruta quale fosse la regola corretta; Gastald invece, in procinto di affondare nell’Oceano del fallimento, riempì un foglio di ghirigori che andavano da cuori avviluppati da nuvole di numeri minacciosi a disegni floreali, tanto arzigogolati da risultare incomprensibili.
            Il silenzio fu interrotto dallo spalancarsi della porta, seguito dalla comparsa del volto corrucciato di Cristine. Non ci vollero parole per capire il motivo di quella irruzione: Gastald si era completamente dimenticato del suo povero paziente che lo attendeva in preda ai tormenti che solo i denti possono regalare. In un attimo si alzò per recarsi in ambulatorio.
         “Amico mio, ci vediamo più tardi da voi, magari con nuove idee” disse a Fabrius andandosene e stringendo in mano i suoi calcoli, senza però un briciolo di speranza. L’amico annuì, sconsolato almeno quanto il dottore, che scomparve in corridoio.
             Quando Gastald giunse in ambulatorio vide con sorpresa che era vuoto. ‘Forse che il paziente stanco per l’attesa se ne fosse andato?’ pensò preoccupato, ma fortunatamente per la sua coscienza un signore anziano, un po’ incurvato dall’età, ma di un’energia straordinaria, sbucò dal suo studio presentandosi. Si era messo a vagare, attratto dai preparati che riposavano in alcune teche. Gastald si scusò per l’imperdonabile ritardo e dal francese farraginoso del suo interlocutore poté solo capire che si trattava di un tal signor Gos, in viaggio di piacere in quella amena regione della Francia; un ascesso improvviso lo aveva costretto ad interrompere il viaggio proprio nel loro paese dove gli avevano detto che avrebbe trovato un medico valente ed efficiente, soggiunse calcando leggermente il tono sull’ultimo aggettivo.
               Gastald lo ignorò e, lavatosi le mani, lo fece accomodare chiedendogli cortesemente di aprire la bocca. La causa del suo problema fu presto individuata: si trattava di un dente malandato, probabilmente da tempo, che avrebbe dovuto estrarre per evitargli altri malesseri. Il paziente, una volta compresa la natura dell’operazione, acconsentì, seppur a malincuore, ed il dottore si mise all’opera. Gli ci volle una buona mezz’ora perché il dente aveva delle radici profonde e non ne voleva sapere di rinunciare al ruolo che aveva avuto da moltissimi anni; alla fine però, con soddisfazione di entrambi gli uomini, dovette arrendersi e terminò la sua carriera in una vaschetta metallica. Dopo altri venti minuti di cure il tutto poteva dirsi terminato con il signor Gos desideroso di specchiarsi per dare un’occhiata al lavoro.
             “Quanto vi defo?” gli domandò in quel suo sgradevole francese. Gastald, che si sentiva in colpa per averlo fatto tanto aspettare, rispose che per quella volta non avrebbe chiesto nulla, come se in seguito potesse ancora avere l’occasione di curare quel paziente di passaggio. Il signor Gos non si diede per vinto e gli avrebbe sicuramente lasciato una generosa manciata di banconote, se non si fosse imbattuto con lo sguardo nei fogli disordinati e pieni di conti del dottore. Doveva essere un tipo sveglio, perché parve capire immediatamente la natura e l’origine di quei calcoli.
              “Aha, das Spielchen das ich als Kind spielte!” disse con un sorriso lieve. “Scusate, quei calcoli mi ricordano la mia giofinezza. Troppo tempo è passato” e la sua fronte si increspò appena, mentre I suoi occhi limpidi riflettevano la soddisfazione per una vita lunga e ben vissuta. Chissà se anche lui avrebbe avuto quello sguardo quando fosse giunto in vista del termine, si chiese il dottore affascinato da quell’uomo. “Ci tenete molto a quei calcoli?”, riprese il suo paziente in tono paterno.
            “Beh, sapete, ho promesso ad una signorina cui tengo molto che avrei risolto quel problema entro stasera e non so veramente come fare” rispose il dottore sorprendendosi nel raccontare ad un perfetto sconosciuto una questione personale.
              “Se c’è ti mezzo una promessa fatta ad una signora, dofete onorarla” rispose l’anziano stringendogli la mano per congedarsi. “Sono certo che troferete la soluzione se saprete guardare dal centro agli estremi e viceversa. In fondo, cosa dicefano gli antichi: in medio stat virus, che fale per tutte le cose della fita se escludete la Fede e l’Amore. Non mi deluderete, ne sono certo, mio caro dottore” aggiunse avviandosi verso l’uscita e a Gastald parve che, prima di volgergli le spalle, gli avesse schiacciato un occhio, ma doveva sicuramente trattarsi di uno scherzo della stanchezza.
               Restato solo si mise a riordinare e pulire gli attrezzi, per poi, sfinito, lasciarsi andare su una sedia osservando le sventurate somme che lo aspettavano, senza fretta, su un foglio posato al centro di un tavolino. ‘Nel mezzo sta la virtù’ pensò il dottore trovandosi perfettamente d’accordo con le due eccezioni sollevate, visto che la Fede è un dono e l’Amore non ammette deroghe.
                ‘Guardare gli estremi’ aggiunse il suo cervello. Cosa intendeva esattamente? Gastald osservò la prima somma che aveva scritto, 1+2=3. aveva solo gli estremi, 1 e 2, che però non gli dicevano molto. La successiva, 1+2+3=6, si rivelò più interessante: gli estremi erano 1 e 3 ed al dottore venne subito spontaneo sommarli ottenendo così 4, ossia il doppio di 2 che era il numero nel mezzo della somma. Qualcosa cominciò a muoversi nella sua testa e, con rinnovata speranza, dopo aver scartato per un momento la somma immediatamente successiva 1+2+3+4=10, passò a considerare con decisione quella dei primi cinque numeri 1+2+3+4+5=15. Questa aveva un 3 nel mezzo e, guarda caso, la somma degli estremi 1 e 5 era proprio 6, cioè il doppio di 3! Non solo, eliminati 1 e 5, i nuovi estremi, 2 e 4 sommati davano nuovamente 6. La somma dei numeri da 1 a 5 si poteva quindi compiere raggruppando gli addendi a due a due, partendo dagli estremi, e sintetizzò questa sua osservazione in questo modo

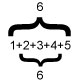
 Passò allora alla somma dei numeri da 1 a 7 (aveva deciso di concentrarsi solo sulla somma di un numero dispari di interi ni modo da avere sempre un numero al centro). Con lo stesso schema si ritrovò a scrivere.
          Dunque,

1 + 2 + 3 + 4 + 5 = 2 ´ 6 + 6/2

mentre

1 + 2 + 3 + 4 + 5 + 6 + 7 = 3 ´ 8 + 8/2

Quanto avrebbe fatto allora la somma dei numeri da 1 a 9, si chiese. Sarà 4 x 10 + 10/2, cioè 45, ipotizzò e subito si mise a fare il calcolo febbrilmente. Era vero: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45! Un rivolo di sudore solcò la fronte di Gastald che comprese di essere ormai vicino alla soluzione. ‘Dunque, se dovessi sommare N numeri, con N dispari, quanto farebbe la somma?’ si domandò e subito scrisse

? ´ (N+1) + (N+1)/2

dove il punto interrogativo si riferiva all’unico fattore che ancora non gli era chiaro. Ora il punto interrogativo valeva 2 per N=5, 3 per N=7 e 4 per N=9. E in generale? Ci pensò a lungo ma alla fine ebbe l’illuminazione: il punto interrogativo era uguale a (N-1)/2. per N=5 trovava infatti (N-1)/2 = 4/2 = 2, per N=7 aveva (N-1)/2 = 6/2=3 ed infine, per N=9, ricavava (N-1)/2 = 8/2 = 4, La formula tanto cercata per N dispari era allora:

somma dei primi N numeri = ½ ´ (N-1) ´ (N+1) + (N+1)/2.

Era tanto felice che non ci pensò due volte a vedere se fosse vera anche per N pari. Prese N=2, lo sostituì nella formula e trovò che restituiva 3, cioè proprio 1+2. Ed anche per N=4 dava il risultato corretto. Verificò che valesse per diversi valori di N e si convinse che aveva trovato la formula che cercava per sommare i primi N numeri interi.
            “Miracoli della matematica”, esclamò ad alta voce fiondandosi per il corridoio e quasi investendo Cristine che, risentita, commentò:
            “Dove andremo a finire, se non c’è più rispetto per la vecchiaia” rifugiandosi in cucina a contemplare un dagherrotipo del dottor Feraud. Gastald, che neanche si accorse dell’incidente, infilò la porta al volo e senza fermarsi, con ben stretto in mano il foglio della formula, giunse all’abitazione di Louise.
            Il campanile batteva le sette quando il dottore prese a picchiare con forza il batacchio dell’uscio. La maestra, che abitava da sola, venne ad aprire poco dopo preoccupata.
           “Oh, siete voi, Maurice. Come state?” gli disse Louise facendolo entrare.
           “Ce l’ho fatta! Ce l’ho fatta, ho risolto il vostro quesito!” esclamò il dottore sventolandole davanti al volto il foglio. Louise si illuminò, lo fece accomodare in soggiorno e ascoltò la spiegazione che Maurice le diede. Al termine, si alzò e trasse un foglietto da un cassetto: su di esso, vergata con la sua elegante calligrafia, stava la soluzione cui anche lei era giunta qualche ora prima.
           “Non credete che sia bellissimo? Abbiamo condiviso la stessa scoperta!” commentò ed era felice quanto bella. “Immagino che voi, che pur dicevate di non aver passione per la matematica, abbiate provato come me un enorme piacere nel giungere alla risposta.”
        Gastald annuì e d’un tratto non pensò alle penose ore passate a scrivere insulse operazioni, né alle delusioni provate, ma soltanto alla soddisfazione di aver risolto il problema.
           “Sapete che vi dico?” proseguì la maestra che aveva riposto il suo foglietto assieme a quello del dottore. “Che dobbiamo festeggiare!” ed il dottore gioì a quella proposta. “E per dei matematici in erba come noi non c’è nulla di meglio che festeggiare con un altro quesito: quanto vale la somma dei quadrati da 1 fino a N? Per domani la risposta?” chiese la maestra con tanta semplicità che quasi il dottore svenne. “Maurice caro, che vi succede? State forse male?” gli domandò premurosa.
            “No, non preoccupatevi, ho solo bisogno di prendere una boccata d’aria” rispose Gastald come deglutendo qualcosa. “Aspettatemi un momento, faccio un breve giro e torno” e, lasciandola, se ne andò tanto rapidamente da non permetterle di precisare che si trattava solo di uno scherzo.
            Certo non poteva dirle che aveva una fretta terribile perché sperava che la carrozza del suo paziente tedesco fosse ancora ferma in paese. “Se riesco a far comprendere a quell’uomo il mio nuovo problema sono sicuro che saprà aiutarmi” pensava infatti il dottore che, pur non sapendo chi fosse, lo considerava un genio. Sfortunatamente per lui quando giunse in piazza della carrozza non restava neppure la polvere sollevata dagli zoccoli dei cavalli. Aveva infatti ripreso già da tempo il suo viaggio con a bordo un suo ex-paziente illustre, il signor Carl Friedrich Gauss** che, curato del mal di denti, si stava concedendo un meritato riposo.

* Nell’originale un evidente errore di stampa: “il numero 1 non alla lettera A ma alla B...”  (nota di XlaTangente)

** Carl Friedrich Gauss (1777-1855) matematico, astronomo e fisico tedesco. Talvolta descritto come “il più grande matematico della modernità” e il “principe della matematica”, Gauss ha contribuito in modo decisivo al progresso della sua disciplina (n. d. r.)

.