Tutti i triangoli sono equilateri

Per dimostrare che tutti i triangoli sono equilateri basta dimostrare che i lati di ogni triangolo sono due a due uguali.

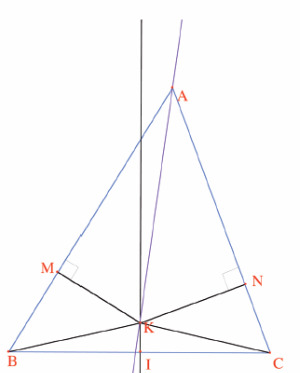
Prendiamo un triangolo «qualunque», come quello qui in figura. Dimostriamo che i lati AB e AC sono uguali. Tracciamo la bisettrice dall’angolo in A e l’asse del segmento BC (e chiamiamo I l’intersezione tra l’asse di BC e BC). Bisettrice e asse del segmento o si intersecano in un punto K (come in figura), o sono parallele.

Se sono parallele, allora la bisettrice è perpendicolare al segmento BC e quindi è anche altezza rispetto al vertice A. Allora si dimostra facilmente che ABC è isoscele in A (e in particolare l’asse di BC coincide con la bisettrice dell’angolo in A). Supponiamo quindi che bisettrice e asse del segmento BC si intersechino come in figura in un punto K e chiamiamo M e N le proiezioni ortogonali di K su AB e su AC rispettivamente. Le proprietà della bisettrice ci assicurano che KM=KN.

Allora i due triangoli rettangoli AMK e ANK, avendo la stessa ipotenusa e una coppia di cateti uguali, sono uguali (Pitagora!) e quindi si ha AM=AN.

Utilizziamo adesso l’ipotesi che K stia sull’asse del segmento BC, per dedurre che KB=KC. Ricordiamo che KM=NK, e consideriamo i triangoli rettangoli KBM e KCN: come nel caso precedente, avendo l’ipotenusa e un cateto di uguali lunghezze, applicando il Teorema di Pitagora si deduce che anche i due cateti restanti, MB e NC, sono uguali tra loro. È il momento di concludere; abbiamo dimostrato che AM=AN e MB=NC. Ne possiamo dedurre che AB=AM+MB =AN+NC=AC, cioè l’uguaglianza che dovevamo dimostrare.

Soluzione