È maggiore la somma dei numeri pari o la somma dei numeri dispari? Questo video di Pavel Boytchev ci mostra due risposte, usando colonnine di mattoni che cercano di riempire dei pozzi. 

Infatti la domanda è equivalente a chiedersi se sommando i numeri dispari e sottraendo i numeri pari si ottiene un numero maggiore, minore o uguale a zero. Le colonnine indicano numeri positivi, i pozzi numeri negativi: inserire una colonnina in un pozzo equivale a sommare i corrispondenti numeri, uno positivo e l'altro negativo. Una volta inserite tutte le colonnine nei pozzi, dobbiamo ancora sommare tutte queste somme parziali. Che risultato otteniamo? 

Nel video vediamo due risultati diversi: le somme parziali possono essere tutte uguali a -1 oppure tutte uguali a +1, quindi la somma totale può essere 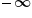 oppure 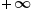. Come è possibile? Ci stiamo sbagliando?

Quelle che stiamo considerando sono serie infinite, cioè somme di sequenze infinite di numeri. Sicuramente conosci già qualche sequenza infinita! Per esempio:

1, 2, 3, 4,...

1, 1, 2, 3, 5, 8,...

-2, -4, -6, -8,...

Avrai forse visto dei quiz di logica che ti chiedono di indovinare il numero successivo in una sequenza costruita secondo una qualche regola nascosta, come questi:

1, 2, 4, 7, 11, ?

3, 8, 6, 11, 9, 14, ?

2, -4 ,-3, 6, 7, -14, -13, ?

I matematici hanno perfino creato un sito con un database in cui vengono riportate tutte le sequenze di numeri interi incontrate in matematica, chiamato Enciclopedia delle Sequenze di Numeri Interi. A ogni sequenza viene dato un nome tramite una sigla; ad esempio i numeri di Fibonacci sono chiamati A000045. Inoltre per ogni sequenza si possono vedere una definizione a parole, le formule (se sono conosciute) per ottenere il termine generico e altri commenti e proprietà.

Qual è la somma di una sequenza infinita di numeri? 

A volte la risposta è semplice: può darsi che la somma sia infinita; questo succede quando, se fissiamo un qualsiasi numero positivo n, per quanto grande sia, la somma di ogni "segmento iniziale" (cioè i primi termini della sequenza) abbastanza lungo è sempre superiore al numero n fissato.  

Per esempio, questo accade sicuramente con quattro delle serie riportate qui sopra, ma anche con la sequenza 1, 1, 1, 1, ... Infatti, fissato un n qualsiasi, se sommiamo i primi n+1 termini otteniamo un numero maggiore di n, e così anche se sommiamo i primi n+2 termini, i primi n+3, ecc.  

Potebbe però succedere anche un fatto analogo con numeri negativi: se fissiamo un qualsiasi numero negativo n, per quanto grande sia in valore assoluto, la somma di ogni segmento iniziale abbastanza lungo è sempre inferiore al numero n fissato. Questo vale per esempio per la terza serie, costituita dai numeri pari negativi.

In entrambi questi casi diciamo che la serie diverge.

Ci sono però serie più interessanti, che hanno somma finita! Eccone una:

1/2, 1/4, 1/8, 1/16, 1/32...

in cui il termine n-esimo vale 1/2ⁿ. Nota che siamo passati a considerare numeri razionali, non più interi.

Quanto vale la somma dei segmenti iniziali di questa serie?

1/2, 1/2+1/4 = 3/4, 1/2+1/4+1/8 = 7/8, 1/2+1/4+1/8+1/16 = 15/16, ...

e così via: la somma n-esima vale (2ⁿ - 1) / 2ⁿ, che è un numero sempre minore di 1! Anzi, per essere più precisi, si avvicina sempre di più a 1, senza mai superarlo, man mano che allunghiamo il segmento iniziale. In questo caso diciamo che la serie converge.

Possiamo visualizzarlo così:

Immaginiamo che il quadrato abbia area 1. Ogni regione del quadrato rappresenta un termine della serie e la sua area è proprio il valore di quel termine. Metà quadrato ha area 1/2 e corrisponde al primo termine della serie. Metà di quello che resta ha area 1/4 e corrisponde al secondo termine della serie.

Si può continuare all'infinito! Il quadrato verrà coperto da piastrelle rettangolari sempre più piccole (ogni volta di area metà della piastrella del passo precedente), ma resterà sempre posto per inserire una nuova piastrella più piccola. Se immaginiamo di inserire infinite piastrelle, possiamo coprire tutto il quadrato. In altre parole, l'area che copriamo con infinite piastrelle (di area 1/2, 1/4, 1/8, ecc) è l'area del quadrato, cioè vale 1.

Tornando alla serie, diremo che essa converge a 1, cioè la somma dei suoi infiniti termini vale proprio 1. Strano, vero? Sommando una quantità infinita di termini, siamo riusciti a produrre un numero finito!

Ma le serie infinite hanno comportamenti ancora più strani! A volte la somma cambia... a seconda dell'ordine in cui applichiamo l'addizione!!! È proprio quello che ci mostra il video di Pavel Boytchev.

Infatti stiamo calcolando 1-2+3-4+5-6+... in due modi diversi: come (1-2)+(3-4)+(5-6)+... che dà (-1)+(-1)+(-1)+..., cioè 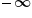, oppure come 1+(-2+3)+(-4+5)+..., che dà 1+1+1+... cioè 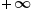. Entrambi i procedimenti sembrano corretti, invece entrambi i risultati sono falsi! 

Il trucco sta nel fatto che la serie non converge: se consideriamo i segmenti iniziali, la loro somma è:

1

1-2 = -1

1-2+3 = 2

1-2+3-4 = -2

1-2+3-4+5 = 3

eccetera. Cioè troviamo alternativamente valori positivi e negativi, e di valore assoluto crescente. In questo caso la serie non converge, cioè la somma dei segmenti iniziali non si avvicina a un valore limite, quindi la somma di tutti gli infiniti termini non è ben definita! In altre parole, non ha senso chiedersi quanto vale, perché si possono ottenere risultati diversi.

Eulero riuscì addirittura a riordinare le somme per mostrare che la serie vale 1/4, cioè un numero non intero! Per saperne di più si può consultare la pagina di Wikipedia dedicata a questa serie.

ED